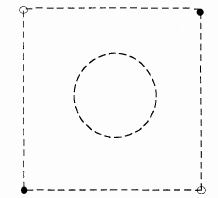
The Unit Cube of the Epola. Tiny light and dark circles represent positrons and electrons;
99.9% of the area is open for passage of nuclear particles. For comparison, the central circle
shows the size of a proton or neutron, of radius 1.1 fermi.
EPOLA: A New Approach to the Fine Structure of Matter and Space
|
Article 7 |
SUBLUMIC, LUMIC, AND SUPERLUMIC MOTION OF NUCLEAR PARTICLES
IN OUR REGION OF THE EPOLA SPACE
1. The Epola Structure of Our Space. All observed phenomena of quantum physics and relativity are physically explained by assuming that space contains electrons and positrons, elastically bound to one another in a rare cubic lattice, the epola. The equilibrium distance between a bound electron and a nearest positron is 4.4 femtometer (fm), fifty times their radii. This distance is four times the radius of a proton or neutron, and equal to the radius of the nucleus of the atom of copper. Atomic bodies can thus move in the epola space, sweeping the nuclei and orbiting electrons of their atoms through the "giving in" distances between the elastically bound epola particles (see article1).

The
Unit Cube of the Epola. Tiny light and dark circles represent positrons and electrons;
99.9% of the area is open for passage of nuclear particles. For comparison, the central circle
shows the size of a proton or neutron, of radius 1.1 fermi.
An epola unit cube expands when entered by a moving nuclear particle and contracts when left by it. This causes the epola particles to vibrate, creating in the epola an elastic electro-magnetic (EM) "accompanying wave"(AW) to the motion of the particle. The AW propagates with the speed of light in a narrow channel ahead of the moving nucleus or electron, pre-forming the epola for the motion in this "wave-guide-like" channel. Thus, when a moving nuclear particle approaches an epola unit cube in the channel, the unit is appropriately expanded to let the particle in, so there is no need for the particle to push epola particles apart "with its own body". Hence, there is no epola resistance to the established motion of the particle, except for the inertial resistance of the epola during the creation of the AW or during any changes in the motion that cause appropriate changes in the AW. To effectively pre-form the epola for the motion of a nuclear particle (and to any changes in the motion), its accompanying epola wave must have sufficient time, hence the velocity of the particle must be adequately lower than the speed of light c, which is that of the AW.
It is easy to see that the vibrational frequency of epola particles in the unit cubes that expand when entered by a moving nuclear particle and contract when left by it, is proportional to the velocity of the particle, and so is also the frequency of the accompanying wave. Therefore, if one wants to accelerate, decelerate, or otherwise change the motion of the particle, then he must accordingly change also the accompanying wave. Thus inertia is a feature not of the moving particle alone but also of the epola particles vibrating in the accompanying wave. Hence, in order to change the motion of a particle, energy must be pumped to overcome the inertial resistance, not only into (or out of) the particle, but also into (or out of) the accompanying epola wave.
2. The Additional Inertial Resistance in Accelerations of Sublumic Electrons.
This additional inertial resistance of the epola becomes significant only at sublumic particle velocities (close to the speed of light c) when the AW arrives to the gate of an epola unit still ahead of the particle, but not sufficient in time to make the unit expand for the arrival of the particle. Hence the fast-moving electron has to push the epola particles apart "with its own body", losing energy of motion.When we accelerate such a fast-moving electron by an electric field and know the force F that the field exerts on an electron, we use Newton's Second Law, a=F/m, to calculate the acceleration a of the electron as the quotient of the force F by the mass me. However the experimentally obtained acceleration is substantially smaller, corresponding by the Second Law to a particle of a substantially larger mass m.
At this point the mathematician among us (or the "theoretical physicist", so called for greater respect and higher pay) to whom Newton's mathematical principles are truly universal and universally true, says that "obviously" the mass of the electron is not a constant but depends on velocity, on the applied field, or on whatever is good for his way of getting a "well working" formula for the outcome. When his "well working" formula disagrees with the "Nature of Things", he announces with ease that "Nature is Absurd", as did the great R.P.Feynman in his 1985 book "QED".
The real physicist, at variance, sticks to Newton's experimentally proven basic concept that "mass is quantitum materiae", so that the mass of the electron or of any other real particle remains constant for as long as nothing and nobody did lick, scratch, or otherwise cut some quantity of matter off the particle. He thus considers the mass values calculated with the Second Law as those of an apparent or effective mass of the electron (term used in solid state physics), takes them seriously and works with them, but looks for physical reasons why do they differ from the real electron mass me. And the physical reason is in the unaccounted for participant, the epola.
3. The Formula for the Apparent Mass of a Sublumic Electron.
We accounted for the additional inertial resistance to sublumic motion by introducing an
additional inertial mass mi , atop of the gravitational mass me
of the electron. Based on our purely physical consideration, we calculated the apparent
or effective mass mv of an electron moving in the epola with
velocity v (in 1985; see the Book, Chapter 17, or the
Paperback, Chapter 8). With a few lines of
freshmen algebra we obtained the formula,
mv = me (1 - v2 / c2 )-1/2
.
The formula yields for the effective mass mv of the electron, orbiting in the hydrogen atom
with velocity v=2,200 km/s (137 times lower than the speed of light c), the
value,
mv = me (1.000027).
This value is larger than the mass me of the electron by less than three thousandths of a
percent only. But a hundred-fold increase in the velocity, to 220,000 km/s, would make the
effective mass of the electron by 46% higher than me . Further increases of the
velocity would drastically increase the mass mv , the more the closer is v to the velocity of light.
It is important to note that we derived the formula for the effective mass mv by compounding the mass me of the electron with the inertial mass mi of the accompanying wave in front of the electron. As there is no such wave atthelumicvelocityv=c=300,000 km/s, this velocity is beyond the applicability limit of our formula. At this velocity of the electron the formula is not valid (yields formally an infinite effective mass of the electron).
4. On Sublumic, Lumic, and Superlumic Motion of Single Nuclear Particles. Just as 'subsonic', 'sonic', and 'supersonic' relates to motion in an elastic medium with velocity, accordingly, below (but not far from) the velocity of sound waves in this medium, equal to, and above the sound velocity, our terms in the Caption relate to motion in space with velocity, accordingly, below (but not far from) the velocity c of light (EM waves) in space, equal to, and above the velocity of light c.
We saw in Chapter 3 that the effective mass mv of an electron moving with velocity v=220,000 km/s is by 46% only higher than the mass me of the electron. At higher sublumic velocities, the effective mass mv increases drastically, due to the drastic increase of the inertial resistance of the epola, when the velocity of the electron is close to the velocity c of the accompanying wave. The wave has no time to pre-form the epola for the motion, the electron has to push apart the epola particles on its way "with its own body", losing energy on it, as also on random collisions with epola particles that had no time to give way.
The velocity of light is also the applicability limit of Einstein's formula for his alleged "dependence of mass on velocity". Using the Maxwell Equations in his derivation, Einstein took with them their hidden contents, the Faraday Dielectric Ether (See articles 5, 6,) and the common resistance of a physical material to motion in it with velocities close to the velocity of its proper elastic waves.
However, Einstein believed in the absolute unlimited power of his formulae; thus, facing the actually not valid "infinite" value of the mass of the electron at v=c, he stated that "Velocities greater than that of light ... have no possibility of existence". Einstein's denial of the possibility of superlumic motion is a result of an improper extrapolation of the power of his formula beyond the limits of its applicability. We know now that electrons and some other nuclear particles can be accelerated to superlumic velocities. Such superlumic particles and phenomena caused by superlumic motions are named "super-relativistic" or "ultra-relativistic", in order not to openly denounce Einstein's statement.
5. Best Superlumic Particles. Electrons and positrons are the best candidates for lumic and superlumic motion, for several good reasons. First, they are easiest to accelerate because of their highest density of electric charge among the stable nuclear particles. The second best here is the proton, having the charge of the positron, but a 1840 times larger mass (and volume) thus a 1840 times lower density of charge.
Second, electrons and positrons are the smallest known stable nuclear particles, of radii (~0.9 fm) that are fifty times smaller than the equilibrium distance between nearest electron and positron, bound in the epola. Their cross-section area for collision with other particles is smallest, and so is their probability to collide with the bound epola particles. Hence, lumic and superlumic electrons or positrons have the longest free paths from among all other nuclear particles that were accelerated to such motions, motions in which there are no accompanying waves to prevent collisions. A lumic or superlumic stable nucleus of diameter close to the diagonal of an epola unit-cube would have a free path no longer than the edge of this unit.
Third, electrons and positrons are the most stable nuclear particles. Even under the now achievable energies of a million MeV, a million times higher than the binding energy per epo pair in the epola, nobody has ever created or destroyed a single electron or a single positron. Hence in a collision with a bound epola particle, a superlumic electron or positron will not disintegrate; it may lose energy and have velocity reduced, down to values at which an accompanying wave is created. At variance, a less stable superlumic nucleus, composed of tens of protons and over twice as many neutrons may not survive its first collision with bound epola particles but undergo a nuclear fission due to a impact higher in energy than the binding of its parts.
Hence, lumic and superlumic motion of single particles of nuclear matter is possible but short-lived: it may last till the first collision with an epola particle. At variance, Superlumic Beams of Nuclear Particles create breakthrough channels in the epola, analogous to breakthrough channels created by a lightning in the air and in insulating solid bodies: bricks, marble, etc. Within the break-through channel, the epola is 'evaporated'; there is no lattice there but separate electrons, positrons, and epo pairs. Collisions with these unbound particles and pairs are fewer and consume much less energy. The energy losses of those particle of the beam which did undergo collisions are promptly replenished by the other particles of the beam, and by their (usually nuclear) source of energy.
If you are interested to find out what the Epola model of space does and can do for the understanding of observed physical phenomena, I may recommend a close encounter with my book Invitation to the Natural Physics of Matter, Space, and Radiation, World Scientific Publishing Co, 1994, (292 pages, ISBN 981-02-1649-1, can be ordered from Amazon.com or Barnes & Noble).
All mathematical
derivations can be found in my Paperback, The
Electron-Positron Lattice Space, Cause of Relativity and Quantum Effects
, Physics Section 5, The Hebrew University, Jerusalem 1990 (158 pages).
The Paperback, as well as my popular Booklet, The Story
of Matter and Space ,1999 (70 pages) can be ordered from Robi Guttman
-
guttmans@netvision.net.il
Write Your Comments in my Guestbook!
![]()
![]()
![]()
Dr. M. Simhony, 33 Shoham Street, 34679 Haifa, Israel
Fax: 972 4 825 1681. E-mail: msimhony@hotmail.com
Top of Page | Home Page | The Booklet | The Paperback | The Book | Publications | Affiliations
More Articles:Updated: 12/2000
Design and
Promotion by Editor of Internet Site: |